파이썬 Numpy(넘파이)

게시 2024/01/30

By KangJJ 43 분읽는 시간

넘파이 (Numpy)

벡터, 행렬 연산을 위한 수치해석용 파이썬 라이브러리
- 강력한 다차원 배열(array) 지원
- 빠른 수치 계산을 위한 structured array, 벡터화 연산, 브로드캐스팅 기법등을 통한 다차원 배열과 행렬연산에 필요한 다양한 함수를 제공한다.
- 파이썬 List 보다 더 많은 데이터를 더 빠르게 처리
많은 과학 연산 라이브러리들이 Numpy를 기반으로 한다.
- scipy, matplotlib, pandas, scikit-learn, statsmodels등
선형대수, 난수 생성, 푸리에 변환 기능 지원

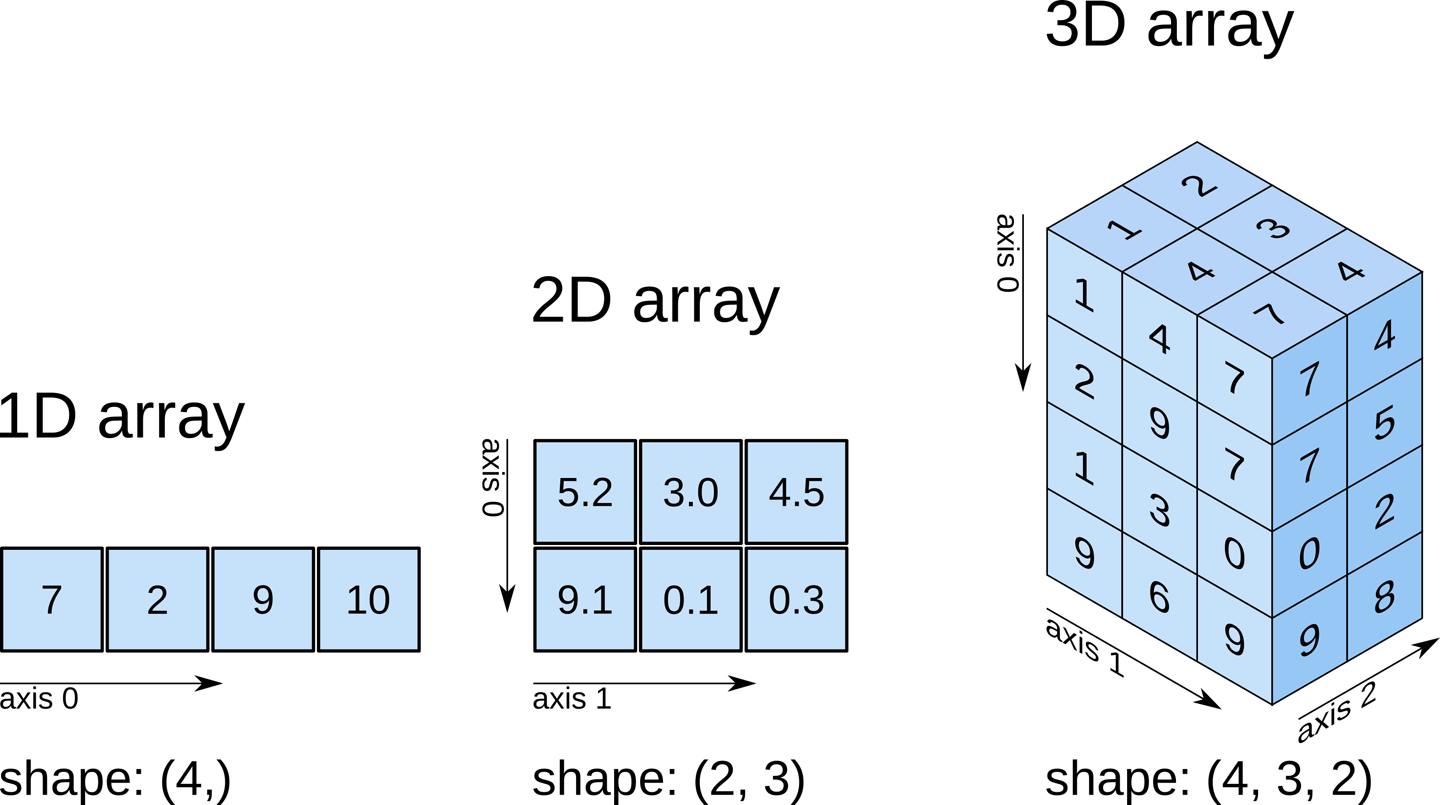
넘파이에서 데이터 구조

스칼라 (Scalar)
- 값 하나.
벡터 (Vector)
- 여러개의 값들을 순서대로 모아놓은 데이터 모음(데이터 레코드)
- 1D Tensor, 1D Array (1차원 배열)
행렬 (Matrix)
- 벡터들을 모아놓은 데이터 집합. 2개의 방향으로 값들이 관리된다.
- 2D Tensor, 2D Array (2차원 배열)
텐서 (Tensor)
- 같은 크기의 행렬들(텐서들)을 모아놓은 데이터 집합. N개의 방향으로 값들이 관리된다.
- ND Tensor, ND Array (다차원 배열)

용어

축 (axis)
- 값들의 나열 방향
- 하나의 축(axis)는 하나의 범주(분류, Category)이다.
랭크 (rank)
- 데이터 집합에서 축의 개수.
- 차원 (dimension) 이라고도 한다.
형태/형상 (shape)
- 각 축(axis) 별 데이터의 개수
크기 (size)
- 배열내 원소의 총 개수

numpy 차원

넘파이 배열(ndarray)

Numpy에서 제공하는 자료구조. N 차원 배열 객체
같은 타입의 값들만 가질 수 있다.
축(Axis)별 데이터의 개수는 모두 동일하다.
빠르고 메모리를 효율적으로 사용하며 벡터 연산과 브로드캐스팅 기능을 제공한다.

차원 (dimension)
Vector에서 차원: 원소의 개수
넘파이 배열에서 차원: 축의 개수

배열 생성 함수

array(iterable [, dtype])

Iterable 객체가 가진 원소들로 구성된 numpy 배열 생성
원하는 값들로 구성된 배열을 만들때 사용한다.
다차원(2차원이상) 배열을 만들 경우 각 axis(축)의 size(데이터의 개수)가 동일하도록 한다.

데이터 타입

원소들의 데이터 타입
ndarray 는 같은 타입의 데이터만 모아서 관리한다.
배열 생성시 dtype 속성을 이용해 데이터 타입 설정 가능
ndarray.dtype 속성을 이용해 조회
ndarray.astype(데이터타입)
데이터타입 변환하는 메소드
변환한 새로운 ndarray객체를 반환
데이터 타입
문자열과 numpy 모듈에서 제공하는 변수를 통해 지정할 수 있다.

Numpy Datatype

분류	문자열	numpy 변수
정수형	“int8”	np.int8
	“int16”	np.int16
	“int32”	np.int32
	“int64”	np.int64
부호없는정수형	“uint8”	np.uint8
	“uint16”	np.uint16
	“uint32”	np.int32
	“uint64”	np.uint64
실수형	“float16”	np.float16
	“float32”	np.float32
	“float64”	np.float64
논리형	“bool”	np.bool
문자열	“str”	np.str

  
import numpy as np

# 원하는 값들로 구성된 배열
a1 = np.array([1,2,3,4,5])
print(type(a1),a1)

<class 'numpy.ndarray'> [1 2 3 4 5]

  
print("원소들의 타입:", a1.dtype)
print("원소 개수:", a1.size)
print("배열의 차원(rank):", a1.ndim)
print("배열의 shape:", a1.shape) # tuple로 리턴

원소들의 타입: int32
원소 개수: 5
배열의 차원(rank): 1
배열의 shape: (5,)

  
# 타입 변경
a2 = a1.astype("float32")
print(a1.dtype, a2.dtype)
print(a2)

int32 float32
[1. 2. 3. 4. 5.]

  
# type 지정, 변환 시 모든 원소들이 가질 수 있는 타입으로 변환해야 함
li = np.array([[1,2]
             ,[3,'a']])
li.astype("int")

---------------------------------------------------------------------------

ValueError                                Traceback (most recent call last)

Cell In[6], line 4
      1 # type 지정, 변환 시 모든 원소들이 가질 수 있는 타입으로 변환해야 함
      2 li = np.array([[1,2]
      3              ,[3,'a']])
----> 4 li.astype("int")


ValueError: invalid literal for int() with base 10: 'a'

동일한 값들로 구성된 배열 생성

zeros(shape [, dtype])

영벡터 생성 : 원소들을 0으로 채운 배열

shape : 형태 지정
- 정수: 1차원일 경우 원소의 개수를 지정
- 튜플: 다차원 배열의 각 축별 size를 설정
dtype : 데이터타입 지정(생략시 float64)

  
a = np.zeros(3)
b = np.zeros((2,2))
c = np.zeros((2,2),dtype=int)
print(f"a = {a} {a.shape} \n b = {b} {b.shape} \n c = {c} {c.shape}")

a = [0. 0. 0.] (3,) 
 b = [[0. 0.]
 [0. 0.]] (2, 2) 
 c = [[0 0]
 [0 0]] (2, 2)

ones(shape [,dtype])

일벡터 생성 : 원소들을 1로 채운 배열을 생성

shape : 형태 지정
- 정수: 1차원일 경우 원소의 개수를 지정
- 튜플: 다차원 배열의 각 축별 size를 설정
dtype : 데이터타입 지정(생략시 float64)

  
a = np.ones(2)
print(a)
print("="*5)
b = np.ones((3,1))
print(b)
print("="*5)
c = np.ones((4,),dtype=int)
print(c)

[1. 1.]
=====
[[1.]
 [1.]
 [1.]]
=====
[1 1 1 1]

full(shape, fill_value [, dtype]))

원소들을 원하는 값으로 채운 배열 생성

shape : 형태 지정
- 정수: 1차원일 경우 원소의 개수를 지정
- 튜플: 다차원 배열의 각 축별 size를 설정
fill_vlaue : 채울 값
dtype : 데이터타입 지정(생략시 float64)

  
a = np.full(shape=(3,1),fill_value = 50)
print(a)

[[50]
 [50]
 [50]]

(zeros, ones, full)_like([ndarray],fill_value)

해당 ndarray와 동일한 shape으로 값을 채운 배열 생성

fill_vlaue(full 인 경우에만) : 채울 값

  
a = np.array([[3,2]
             ,[1,10]])
print(a.shape,end="\n=====\n")

x = np.zeros_like(a)
print(x, x.shape,end="\n=====\n")
y = np.ones_like(a)
print(y,y.shape,end="\n=====\n")
z = np.full_like(a,fill_value = 5)
print(z,z.shape)

(2, 2)
=====
[[0 0]
 [0 0]] (2, 2)
=====
[[1 1]
 [1 1]] (2, 2)
=====
[[5 5]
 [5 5]] (2, 2)

특정 범위내에서 동일한 간격의 값들로 구성된 배열생성

arange(start, stop, step, dtype)

start에서 stop 범위에서 step의 일정한 간격의 값들로 구성된 배열 리턴. 1차원 배열만 생성할 수 있다. (list의 range()와 비슷한 기능의 함수)

start : 범위의 시작값으로 포함된다.(생략가능 - 기본값:0)
stop : 범위의 끝값으로 포함되지 않는다. (필수)
step : 간격 (기본값 1)
dtype : 요소의 타입
1차원 배열만 생성가능

  
#기본값은 Stop으로 적용
a = np.arange(10)
print(a,end="\n=====\n")

# 1부터 9까지 2.5 간격으로
b = np.arange(1,10,2.5)
print(b)

[0 1 2 3 4 5 6 7 8 9]
=====
[1.  3.5 6.  8.5]

linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)

시작과 끝을 균등하게 나눈 값들을 가지는 배열을 생성

start : 시작값
stop : 종료값
num : 나눌 개수. 기본-50, 양수 여야한다.
endpoint : stop을 포함시킬 것인지 여부. 기본 True
retstep : 생성된 배열 샘플과 함께 간격(step)도 리턴할지 여부. True일경우 간격도 리턴(sample, step) => 튜플로 받는다.
dtype : 데이터 타입
1차원 배열만 생성가능

  
# 0부터 10까지 50개로 나눈 배열
a = np.linspace(0,10)
print(a)

[ 0.          0.20408163  0.40816327  0.6122449   0.81632653  1.02040816
2244898   1.42857143  1.63265306  1.83673469  2.04081633  2.24489796
44897959  2.65306122  2.85714286  3.06122449  3.26530612  3.46938776
67346939  3.87755102  4.08163265  4.28571429  4.48979592  4.69387755
89795918  5.10204082  5.30612245  5.51020408  5.71428571  5.91836735
12244898  6.32653061  6.53061224  6.73469388  6.93877551  7.14285714
34693878  7.55102041  7.75510204  7.95918367  8.16326531  8.36734694
57142857  8.7755102   8.97959184  9.18367347  9.3877551   9.59183673
79591837 10.        ]

  
# 0부터 10까지 20개로 나눈 배열에 10을 포함하지 않음
b = np.linspace(0,10,num=20,endpoint = False)
print(b)

[0.  0.5 1.  1.5 2.  2.5 3.  3.5 4.  4.5 5.  5.5 6.  6.5 7.  7.5 8.  8.5
 9.  9.5]

  
# 0부터 20까지 40개로 나눈 배열에 20을 포함하지않고, 간격값을 리턴.
c = np.linspace(0,20,num=40,endpoint=False,retstep=True)
print(c) # 간격은 0.5임

(array([ 0. ,  0.5,  1. ,  1.5,  2. ,  2.5,  3. ,  3.5,  4. ,  4.5,  5. ,
        5.5,  6. ,  6.5,  7. ,  7.5,  8. ,  8.5,  9. ,  9.5, 10. , 10.5,
       11. , 11.5, 12. , 12.5, 13. , 13.5, 14. , 14.5, 15. , 15.5, 16. ,
       16.5, 17. , 17.5, 18. , 18.5, 19. , 19.5]), 0.5)

난수(Random value)를 원소로 하는 ndarray 생성

numpy의 서브패키지인 random 패키지에서 제공하는 함수들을 이용해 생성

np.random.seed(시드값)

난수 발생 알고리즘이 사용할 시작값(시드값)을 설정
시드값을 설정하면 항상 일정한 순서의 난수(random value)가 발생한다.
랜덤함수는 특정숫자부터 시작하는 일렬의 수열을 만들어 값을 제공하는 함수이다.
시작 숫자는 실행할때 마다 바뀌므로 다른 값들이 나오는데 시드값은 시작값을 고정시키면 항상 시작 값이 같으므로 같은 값들이 순서대로 제공된다.
매번 실행할때 마다 같은 순서의 임의의 값이(난수) 나오도록 할때 시드값을 설정한다.

  
np.random.seed(0)

np.random.rand([axis0, axis1, axis2, …])

0~1사이의 실수를 리턴
축의 크기는 순서대로 나열한다.

  
a = np.random.rand(5) # (5,)인 배열 리턴
print(a,a.shape,end="\n=======\n")
b = np.random.rand(5,2) # 5,2)인 배열 리턴
print(b,b.shape)

[0.63992102 0.14335329 0.94466892 0.52184832 0.41466194] (5,)
=======
[[0.26455561 0.77423369]
 [0.45615033 0.56843395]
 [0.0187898  0.6176355 ]
 [0.61209572 0.616934  ]
 [0.94374808 0.6818203 ]] (5, 2)

np.random.normal(loc=0.0, scale=1.0, size=None)

정규분포를 따르는 난수.

loc: 평균
scale: 표준편차
loc, scale 생략시 표준정규 분포를 따르는 난수를 제공

  
# shape이 (5,)이고 표준정규분포를 따르는 값들의 배열 추출
print(np.random.normal(size = 5))

[-0.63432209 -0.36274117 -0.67246045 -0.35955316 -0.81314628]

  
# shape이 (2,4), 값들의 평균은 100, 표준편차는 50인 정규분포를 따르는 값들을 랜덤 추출
print(np.random.normal(loc=100,scale = 50, size = (2,4)))

[[102.80826711  41.74250796 145.04132435 123.28312199]
 [ 23.18781569 174.41260969 194.7944588  158.93897856]]

정규분포
평균: 데이터셋의 값들을 대표하는 값중 하나로 모두 더해서 개수로 나눈 것.
정규분포에서 값들이 가장 많이 있을 것이라 생각되는 값이 평균이므로 대푯값으로 사용한다.
편차: 데이터셋의 각 값들이 평균과 얼마나 차이가 있는지
표준편차: 편차의 평균 (평균으로 부터 각 값들이 얼마나 떨어져 있는지에 대한 평균)
분산: 표준편차의 제곱으로 표준편차 계산시 나오는 값.
분포: 값이 흩어져 있는 상태를 말한다.
정규분포
연속 확률 분포중 하나. 우리생활에서 가장 많이 나오는 분포중 하나로 종모양을 하고 있으며 평균근처에 가장 많은 값들이 모여 있고 평균으로 부터 표준편차 많큼 멀어질 수록 적게 분포된다.
정규분포에서는 1표준편차 범위의 전체 데이터의 68%가 2표준편차 범위에 전체 데이터의 95% 정도가 분포한다. (3표준편차범위에 약 99.7%가 분포)
표준정규분포
평균 : 0, 표준편차 : 1 인 정규 분포
정규분포는 평균과 표준편차로 표현한다.

  
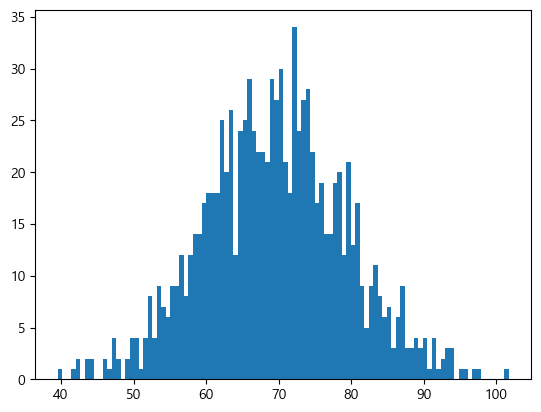
# shape은 (1000,) 평균은 70, 표준편차는 10인 정규분포 내 랜덤 값들의 정규 분포 그래프
import matplotlib.pyplot as plt

v = np.random.normal(loc=70,scale=10,size=1000)
plt.hist(v,bins=100)
plt.show()

np.random.randint(low, high=None, size=None, dtype=’int32’)

임의의 정수를 가지는 배열

low ~ high 사이의 정수 리턴. high는 포함안됨
high 생략시 0 ~ low 사이 정수 리턴. low는 포함안됨
size : 배열의 크기. 다차원은 튜플로 지정 기본 1개
dtype : 원소의 타입

  
# 0 ~ 10까지 랜덤값 추출
np.random.randint(11)

10

  
# 30 ~ 50 까지 랜덤 정수값을 shape이 (2,3,2)인 배열로 추출
np.random.randint(low=30,high=51,size=(2,3,2))

array([[[47, 36],
        [42, 38],
        [38, 38]],

       [[42, 35],
        [48, 32],
        [35, 35]]])

np.random.choice(a, size=None, replace=True, p=None)

샘플링(표본추출) 메소드
a : 샘플링대상. 1차원 배열 또는 정수 (정수일 경우 0 ~ 정수, 정수 불포함)
size : 샘플 개수
replace : True-복원추출(기본), False-비복원추출
p: 샘플링할 대상 값들이 추출될 확률 지정한 배열

  
# 1 ~ 10까지 배열에서 랜덤값을 비복원 추출하여 shape (5,)인 배열 값을 생성
np.random.choice(11,size=5,replace=False)

array([7, 4, 5, 6, 2])

  
# 30 ~ 35까지 값을 추출하되 복원 추출을 시행하며, shape이 (3,3,3) 으로 추출. 
# 30 : 10% , 31 : 15%, 32 : 17%, 33 : 23%, 34 : 20%, 35 : 15% 확률로 설정
np.random.choice(range(30,36),size=(3,3,3),p=[0.1,0.15,0.17,0.23,0.2,0.15])

array([[[35, 33, 30],
        [31, 32, 33],
        [34, 32, 34]],

       [[34, 32, 35],
        [33, 35, 33],
        [34, 34, 35]],

       [[31, 33, 33],
        [35, 31, 35],
        [35, 30, 33]]])

인덱싱과 슬라이싱을 이용한 배열의 원소 조회 및 변경

배열 인덱싱(Indexing)

index
- 배열내의 원소의 식별번호
- 0부터 시작
indexing – index를 이용해 원소 조회
- [] 표기법 사용
구문
- ndarray[index]
- 양수는 지정한 index의 값을 조회한다.
- 음수는 뒤부터 조회한다.
  - 마지막 index가 -1
- 2차원배열의 경우
  - arr[0축 index, 1축 index]
  - 파이썬 리스트와 차이점
- N차원 배열의 경우
  - arr[0축 index, 1축 index, …, n축 index]
팬시(fancy) 인덱싱
- 여러개의 원소를 한번에 조회할 경우 리스트에 담아 전달한다.
- 다차원 배열의 경우 각 축별로 list로 지정
- arr[[1,2,3,4,5]]
  - 1차원 배열(vector): 1,2,3,4,5 번 index의 원소들 한번에 조회
- arr[[0,3], [1,4]]
  - [0,3] - 1번축 index list, [1,4] - 2번축 index list
  - 2차원 배열(matrix): [0,1], [3,4] 의 원소들 조회

  
import numpy as np
a= np.random.randint(1,10,size=(3,5))
print(a)

[[5 8 9 8 8]
 [1 7 4 8 3]
 [7 4 6 9 6]]

  
# axis0 = 1, axis1 = 2인 값 출력
# 기존 리스트 사용법
print(a[1][2])

# 2차원 배열
# a[0축 index, 1축 index]
print(a[1,2])

4
4

  
b = np.random.randint(1,10,size=(3,2,5))
b

array([[[1, 7, 2, 5, 8],
        [6, 3, 7, 5, 8]],

       [[4, 7, 8, 1, 7],
        [5, 3, 4, 3, 1]],

       [[6, 9, 2, 1, 6],
        [3, 2, 4, 1, 7]]])

  
# axis0 모든 것들에 대해 axis1 = 1인 값들 출력
b[:,1]

array([[6, 3, 7, 5, 8],
       [5, 3, 4, 3, 1],
       [3, 2, 4, 1, 7]])

  
np.random.seed(0)
c = np.random.randint(1,10,size=10)
print(c)

# 0,2,5 번째 index의 값 구하기
print(c[[0,2,5]])  # c[0,2,5] 는 error : 3차원으로 인식하기 때문.

[6 1 4 4 8 4 6 3 5 8]
[6 4 4]

  
a= np.random.randint(1,10,size=(3,5))
print(a)

print(a[0,[1,4]]) # 0번째 인덱스 배열의 1,4 번 인덱스 값

[[4 3 8 3 1]
 [1 5 6 6 7]
 [9 5 2 5 9]]
[3 1]

  
# axis0 = 0의  axis1 = 0인 값과 axis0=2의 axis1 = 4인 값 가져오기
a[[0,2],[0,4]] # 0 -0 , 1 - 4 매치

array([4, 9])

  
# axis0 값이 0에 대해 axis1 값이 0,4인 값과 axis0 값이 2에 대해 axis1 =1,2인 값 가져오기
a[[[0],[2]],[[0,4],[1,2]]]

array([[4, 1],
       [5, 2]])

슬라이싱

배열의 원소들을 범위로 조회한다.
ndarry[start : stop : step ]
- start : 시작 인덱스. 기본값 0
- stop : 끝 index. stop은 포함하지 않는다. 기본값 마지막 index
- step : 증감 간격. 기본값 1

다차원 배열 슬라이싱

각 축에 slicing 문법 적용
2차원의 경우
- arr [0축 slicing, 1축 slicing]
  - arr[:3, :]
- , 로 축을 구분한 다중 슬라이싱 사용
다차원의 경우
- arr[0축 slicing, 1축 slicing, …, n축 slicing]
slicing과 indexing 문법은 같이 쓸 수 있다.

  
c = np.arange(10)

print(c[:])
print(c[5:])
print(c[::2])
print(c[:1:-2])

[0 1 2 3 4 5 6 7 8 9]
[5 6 7 8 9]
[0 2 4 6 8]
[9 7 5 3]

  
b = np.random.randint(1,10,size=(3,2,5))
b

array([[[2, 2, 8, 4, 7],
        [8, 3, 1, 4, 6]],

       [[5, 5, 7, 5, 5],
        [4, 5, 5, 9, 5]],

       [[4, 8, 6, 6, 1],
        [2, 6, 4, 1, 6]]])

  
# 모든 axis0에 대해 axis1 = 0이고, axis2 = 1인 요소들 가져오기
print(b[:,0,1])

[2 5 8]

  
# 모든 axis0,axis1에 대해 axis2 = 0인 값 가져오기
x = b[:,:,1]
print(x,end="\n=====\n")

# 차원이 줄어듬
print(x.shape)

[[2 3]
 [5 5]
 [8 6]]
=====
(3, 2)

  
# 차원이 변경되지 않음
y = b[:,:,[1]]
print(y,end="\n=====\n")
print(y.shape)

[[[2]
  [3]]

 [[5]
  [5]]

 [[8]
  [6]]]
=====
(3, 2, 1)

boolean indexing

Index 연산자에 같은 형태(shape)의 Boolean 배열을 넣으면 True인 index의 값만 조회 (False가 있는 index는 조회하지 않는다.)
ndarray내의 원소 중에서 원하는 조건의 값들만 조회할 때 사용
- ndarray는 element-wise 연산을 지원한다. 이를 이용해 boolean indexing으로 원하는 조건의 값들을 조회할 수 있다.
boolean indexing을 masking이라고도 한다.

넘파이 비교연산자

파이썬의 and, or, not은 사용할 수 없다.
&: and연산
|: or 연산
~: not 연산
피연산자는 ( )로 묶어야 한다.

  
c = c = np.arange(10)
flag = np.random.choice([True,False],size=10)
flag

array([ True, False,  True, False, False, False, False,  True,  True,
        True])

  
# c중에서 True인 인덱스의 값만 추출
c[flag]

array([0, 2, 7, 8, 9])

  
# c값중 5보다 큰것만 추출
c[c>5]

array([6, 7, 8, 9])

  
a= np.random.randint(1,10,size=(3,5))
print(a)

[[8 3 3 4 4]
 [3 4 5 2 3]
 [2 5 7 9 3]]

  
# a의 값들 중 2 이상 6이하 값들만 추출
a[(a>=2)&(a<=6)]

array([3, 3, 4, 4, 3, 4, 5, 2, 3, 2, 5, 3])

  
# 2작거나 6보다 큰 값들만 추출
## 방법1. AND(&) , NOT(~) 사용
print(a[~((a >= 2)&(a<=6))],end="\n====\n")
## 방법2. OR(|) 사용
print(a[(a<2) | (a>6)])

[8 7 9]
====
[8 7 9]

조건을 만족하는 값들은 알 수 있지만, 해당 값의 위치(인덱스)는 모름

np.where()

True의 index 조회
- np.where(boolean 배열) - True인 index를 반환
  - 반환타입: Tuple . True인 index들을 담은 ndarray를 축별로 Tuple에 묶어서 반환한다.
- boolean연산과 같이사용하여 배열내에 특정 조건을 만족하는 값들을 index(위치)를 조회할 때 사용한다.
True와 False를 다른 값으로 변환
- np.where(boolean 배열, True를 대체할 값, False를 대체할 값)
  - 배열내의 True를 True를 대체할 값으로 False를 False를 대체할 값 으로 변환한다.

  
# 값이 참인 곳의 인덱스 추출
np.where([True,False,True])

(array([0, 2], dtype=int64),)

  
c = np.arange(10)
print(c)
np.where(c>5)[0] # 5보다 큰 값들의 인덱스

[0 1 2 3 4 5 6 7 8 9]

array([6, 7, 8, 9], dtype=int64)

  
a= np.random.randint(1,10,size=(3,5))
print(a)

[[4 1 1 7 1]
 [7 4 4 9 9]
 [9 3 4 3 1]]

  
# a에서 5보다 큰 값들의 axis0 과 axis1 축
np.where(a>5)

(array([0, 1, 1, 1, 2], dtype=int64), array([3, 0, 3, 4, 0], dtype=int64))

  
# a에서 5보다 큰 값들의 인덱스
for x,y in zip(*np.where(a>5)):
    print(f"({x},{y}) = {a[x,y]}")

(0,3) = 7
(1,0) = 7
(1,3) = 9
(1,4) = 9
(2,0) = 9

  
b = np.random.randint(1,10,size=(3,2,5))
print(b,end = "\n=========\n")
for x,y,z in zip(*np.where(b>5)):
    print(f"({x},{y},{z}) = {b[x,y,z]}")

[[[9 7 7 2 7]
  [9 9 4 3 4]]

 [[7 4 7 6 8]
  [1 9 5 7 6]]

 [[9 3 4 8 6]
  [4 5 6 4 4]]]
=========
(0,0,0) = 9
(0,0,1) = 7
(0,0,2) = 7
(0,0,4) = 7
(0,1,0) = 9
(0,1,1) = 9
(1,0,0) = 7
(1,0,2) = 7
(1,0,3) = 6
(1,0,4) = 8
(1,1,1) = 9
(1,1,3) = 7
(1,1,4) = 6
(2,0,0) = 9
(2,0,3) = 8
(2,0,4) = 6
(2,1,2) = 6

  
a = np.arange(10)
print(a)

[0 1 2 3 4 5 6 7 8 9]

  
# a의 값중 5보다 작으면 -99, 아니면 1로 변경
np.where(a<5,-99,1)

array([-99, -99, -99, -99, -99,   1,   1,   1,   1,   1])

기타

np.any(boolean 배열)
- 배열에 True가 하나라도 있으면 True 반환
- 배열내에 특정조건을 만족하는 값이 하나 이상 있는지 확인할 때 사용
np.all(boolean 배열)
- 배열의 모든 원소가 True이면 True 반환
- 배열내의 모든 원소가 특정 조건을 만족하는지 확인 할 때 사용
특정 조건이 True인 값들을 조회 -> boolean indexing
특정 조건이 True인 값들의 index -> np.where()
특정 조건의 값이 하나라도 있는지 -> np.any()
모든 값들이 특정 조건을 만족하는지(True) -> np.all()

  
# a의 모든 요소가 모두 양수인지 여부
a = np.arange(10)
np.all(a>=0)

True

  
# a의 모든 요소가 2보다 큰지 여부
np.all(c>2)

False

  
# a의 요소 중 8보다 큰값이 하나라도 있는가
np.any(a>8)

True

  
# a의 요소 중 20보다 큰게 있는가
np.any(a > 20)

False

배열의 형태(shape) 변경

배열의 원소의 개수를 유지하는 상태에서 shape을 변경할 수있다.
- 예) (16, ) -> (4,4) -> (2,2,4) -> (2,2,2,2), -> (4,4,1) -> (1, 16)

reshape()을 이용한 차원 변경

numpy.reshape(a, newshape) 또는 ndarray.reshape(newshape)
- a: 형태를 변경할 배열
- newshape : 변경할 형태 설정.
  - 원소의 개수를 유지하는 shape으로만 변환 가능하다.
  - 각 axis(축)의 size를 지정할 때 하나의 축의 size를 -1로 줄 수있다. 그러면 알아서 축 size를 설정해 준다. (전체 size / 지정한 axis들 size의 곱)
- 둘다 원본을 바꾸지 않고 reshape한 새로운 배열을 만들어 반환한다.

  
# shape이 (100,)인 1차원 배열을 (2,50)으로 변경
a = np.arange(100).reshape(2,-1)
print(a.shape)
display(a)

(2, 50)



array([[ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11, 12, 13, 14, 15,
        16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31,
        32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47,
        48, 49],
       [50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65,
        66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81,
        82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97,
        98, 99]])

  
a2 = a.reshape(10,2,5)
a2.shape

(10, 2, 5)

  
a3 = a.reshape(5,2,2,-1)
a3.shape

(5, 2, 2, 5)

  
a3.reshape(2,10) #개수가 안맞으므로 Error

---------------------------------------------------------------------------

ValueError                                Traceback (most recent call last)

Cell In[120], line 1
----> 1 a3.reshape(2,10)

ValueError: cannot reshape array of size 100 into shape (2,10)

차원 늘리기(확장)

Dummy axis(축)을 늘린다.
- Dummy axis: size가 1인 axis 를 말한다.
reshape() 을 이용해 늘릴 수 있다.

  
a = np.arange(100).reshape(-1,50)
print(a)

[[ 0  1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23
  24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
  48 49]
 [50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73
  74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97
  98 99]]

  
# (2,50) -> (1,2,50)
b = a.reshape(1,2,50) # 기존 데이터의 shape을 확인해야하는 단점이 있음.
print(b.shape)

(1, 2, 50)

indexer와 np.newaxis 변수를 이용해 늘린다.
- ndarray[…, np.newaxis] 또는 ndarray[np.newaxis, …]
  - 맨앞 또는 맨 마지막에 dummy axis(축)을 늘릴때 사용한다.
  - 축을 늘리려는 위치에 np.newaxis를 지정하고 ... 으로 원본 배열의 shape을 유지함을 알려준다.
np.expand_dims(대상배열, axis=늘릴축)
- dummy axis를 원하는 axis에 추가한다.

  
a[np.newaxis,...,np.newaxis].shape

(1, 2, 50, 1)

  
print(np.expand_dims(a,0).shape)
print(np.expand_dims(a,1).shape) # 중간에 차원 확장 가능
print(np.expand_dims(a,-1).shape)
print(np.expand_dims(a,[0,2,-1]).shape) # 여러 축 확장 가능

(1, 2, 50)
(2, 1, 50)
(2, 50, 1)
(1, 2, 1, 50, 1)

Dummy 축(axis) 줄이기(축소)

numpy.squeeze(배열, axis=None), 배열객체.squeeze(axis=None)

배열에서 지정한 축(axis)을 제거하여 차원(rank)를 줄인다.
제거하려는 축의 size는 1이어야 한다.
축을 지정하지 않으면 size가 1인 모든 축을 제거한다.
- (3,1,1,2) => (3,2)

  
print(b.shape)
print(b.squeeze().shape) # dummy축을 제거하여 축소

(1, 2, 50)
(2, 50)

  
x = np.expand_dims(a,[0,2,-1])
print(x.shape)
print(x.squeeze(axis=2).shape) # 특정차원의 axis를 지정하여 축소 가능

(1, 2, 1, 50, 1)
(1, 2, 50, 1)

배열객체.flatten()

다차원 배열을 1차원으로 만든다.

  
print(a.shape)
print(a.reshape(-1,).shape)
print(a.flatten().shape) # N차원을 1차원으로

(2, 50)
(100,)
(100,)

  
print(a2.shape)
print(a2.reshape(-1,).shape)
print(a2.flatten().shape)

(10, 2, 5)
(100,)
(100,)

배열 연산

벡터화 - 벡터 연산

배열과 scalar 간의 연산은 원소단위로 계산한다.
배열간의 연산은 같은 index의 원소끼리 계산 한다.
- Element-wise(원소별) 연산 이라고도 한다.
- 배열간의 연산시 배열의 형태(shape)가 같아야 한다.
- 배열의 형태가 다른 경우 Broadcast 조건을 만족하면 연산이 가능하다.

배열과 스칼라간 연산

\[\begin{align} 10 - \begin{bmatrix} 1 \\ 2 \\ 3 \\ \end{bmatrix} = \begin{bmatrix} 10 - 1 \\ 10 - 2 \\ 10 - 3 \\ \end{bmatrix} = \begin{bmatrix} 9 \\ 8 \\ 7 \\ \end{bmatrix} \end{align}\] \[\begin{align} 10 \times \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} 10\times1 & 10\times2 \\ 10\times3 & 10\times4 \\ \end{bmatrix} = \begin{bmatrix} 10 & 20 \\ 30 & 40 \end{bmatrix} \end{align}\]

배열 간의 연산

\[\begin{align} \begin{bmatrix} 1 \\ 2 \\ 3 \\ \end{bmatrix} + \begin{bmatrix} 10 \\ 20 \\ 30 \\ \end{bmatrix} = \begin{bmatrix} 1 + 10 \\ 2 + 20 \\ 3 + 30 \\ \end{bmatrix} = \begin{bmatrix} 11 \\ 22 \\ 33 \\ \end{bmatrix} \end{align}\] \[\begin{align} \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} + \begin{bmatrix} 10 & 20 \\ 30 & 40 \\ \end{bmatrix} = \begin{bmatrix} 1+10 & 2+20 \\ 3+30 & 4+40 \end{bmatrix} = \begin{bmatrix} 11 & 22 \\ 33 & 44 \end{bmatrix} \end{align}\]

  
import numpy as np

a = np.arange(3)
b = np.arange(10,13)
c = np.arange(5)
print(a.shape,b.shape,c.shape)

(3,) (3,) (5,)

  
print(a)
print(a+100)
print(a > 5)

[0 1 2]
[100 101 102]
[False False False]

  
print(a)
print(b,end="\n===========\n")
print(a+b)
print(a*b)

[0 1 2]
[10 11 12]
===========
[10 12 14]
[ 0 11 24]

내적 (Dot product) 연산

@ 연산자 또는 numpy.dot(벡터/행렬, 벡터/행렬) 함수 사용
같은 index의 원소끼리 곱한뒤 결과를 모두 더한다.
벡터간의 내적의 결과는 스칼라가 된다.
$ x \cdot y $ 또는 $x^T y$로 표현
조건
- 두 벡터의 차원(원소의개수)가 같아야 한다.
- 앞의 벡터는 행벡터 뒤의 벡터는 열벡터 이어야 한다.
  - numpy 에서는 vector 끼리 연산시 앞의 벡터는 행벡터로 뒤의 벡터는 열벡터로 인식해 처리한다.

\[\begin{align} x = \begin{bmatrix} 1 \\ 2 \\ 3 \\ \end{bmatrix} ,\;\;\; y = \begin{bmatrix} 4 \\ 5 \\ 6 \\ \end{bmatrix} \end{align}\] \[\begin{align} x^T y = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} \begin{bmatrix} 4 \\ 5 \\ 6 \\ \end{bmatrix} = 1 \times 4 + 2 \times 5 + 3 \times 6 = 32 \end{align}\]

행렬 곱

같은 index의 앞 행렬의 행과 뒤 행렬의 열간에 내적을 한다.
행렬과 행렬을 내적하면 그 결과는 행렬이 된다.
앞 행렬의 열수와 뒤 행렬의 행수가 같아야 한다.
내적의 결과의 형태(shape)는 앞행렬의 행수와 뒤 행렬의 열의 형태를 가진다.
- (3 x 2)와 (2 x 5) = (3 x 5)
- (1 x 5)와 (5 x 1) = (1 x 1)

\[\begin{align} A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \end{align}\] \[\begin{align} B = \begin{bmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \end{bmatrix} \end{align}\] \[\begin{align} A\cdot B = \begin{bmatrix} 1\times 1 + 2\times 3 + 3 \times 5 & 1\times 2 + 2\times 4 + 3 \times 6 \\ 4\times 1 + 5\times 3 + 6 \times 5 & 4\times 2 + 5\times 4 + 6 \times 6 \end{bmatrix} = \begin{bmatrix} 22 & 28 \\ 49 & 64 \end{bmatrix} \end{align}\]

내적의 예

가중합

가격: 사과 2000, 귤 1000, 수박 10000
개수: 사과 10, 귤 20, 수박 2
총가격?
2000*10 + 1000 * 20 + 10000 * 2

  
price = np.array([2000,1000,10000])
cnt = np.array([10,20,2])
print(price@cnt) # @ 연산자 사용
print(np.dot(price,cnt)) # np.dot 사용

60000
60000

  
price = np.array([[2000,1000,10000]])
cnt = np.array([[10]
       ,[20]
       ,[2]])

  
print(price.shape,cnt.shape)

(1, 3) (3, 1)

  
(price @ cnt).shape # 첫번째의 axis0 * 두번째의 axis1 과 같음

(1, 1)

  
price = np.array([[2000,1000,10000]])
cnt = np.array([
        [10,5,20,10]
       ,[20,7,15,20]
       ,[2,10,10,2]])

  
print(price.shape,cnt.shape)

(1, 3) (3, 4)

  
result = price@cnt
print(result,result.shape,sep="\n")

[[ 60000 117000 155000  60000]]
(1, 4)

기술통계함수

통계 결과를 계산해 주는 함수들
구문
1. np.전용함수(배열)
  - np.sum(x)
2. 일부는 배열.전용함수() 구문 지원
  - x.sum() - 공통 매개변수
  - axis=None: 다차원 배열일 때 통계값을 계산할 axis(축)을 지정한다. None(기본값)은 flatten후 계산한다.
배열의 원소 중 누락된 값(NaN - Not a Number) 있을 경우 연산의 결과는 NaN으로 나온다.
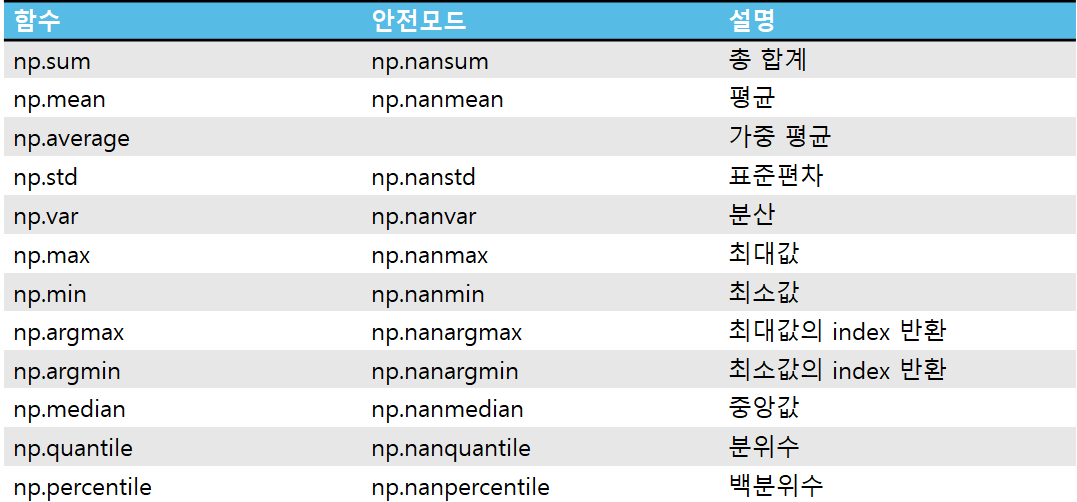
안전모드 함수
- 배열내 누락된 값(NaN)을 무시하고 계산
https://docs.scipy.org/doc/numpy-1.15.1/reference/routines.statistics.html

  
a = np.array([3,6,9,np.nan])
b = np.array([10,20,30])

print(np.sum(b))

60

  
print(np.sum(a)) # 결측치 포함
print(np.nansum(a)) #결측치 제외

nan
18.0

  
np.average(b,weights=[2,3,1]) # weights = 각 요소별 가중치

18.333333333333332

  
w = np.array([2,3,1])
print(b.shape,w.shape)
(b@w) / np.sum(w)

(3,) (3,)

18.333333333333332

브로드캐스팅

사전적의미 : 퍼트린다. 전파한다.
형태(shape)가 다른 배열 연산시 배열의 형태를 맞춰 연산이 가능하도록 한다.
- 모든 형태를 다 맞추는 것은 아니고 조건이 맞아야 한다.
조건
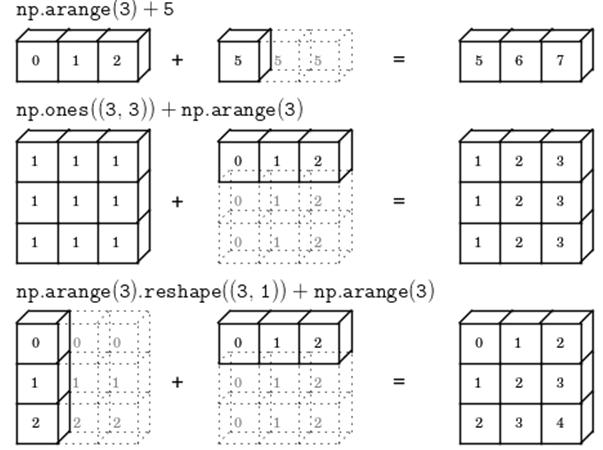
1. 두 배열의 축의 개수가 다르면 작은 축의개수를 가진 배열의 형태(shape)의 앞쪽을 1로 채운다.
  - (2, 3) + (3, ) => (2, 3) + (1, 3)
2. 두 배열의 차원 수가 같지만 각 차원의 크기가 다른 경우 어느 한 쪽에 1이 있으면 그 1이 다른 배열의 크기와 일치하도록 늘어난다.
  - 1 이외의 나머지 축의 크기는 같아야 한다.
  - 늘리면서 원소는 복사한다.
  - (2, 3) + (1, 3) => (2, 3)+(2, 3)

  
x = np.arange(18).reshape(3,2,3)
y = np.arange(18).reshape(3,2,3)
z = np.arange(18).reshape(3,3,2)

  
print(x+y)

[[[ 0  2  4]
  [ 6  8 10]]

 [[12 14 16]
  [18 20 22]]

 [[24 26 28]
  [30 32 34]]]

  
print(x>y)

[[[False False False]
  [False False False]]

 [[False False False]
  [False False False]]

 [[False False False]
  [False False False]]]

  
x + z # 차원 구조가 다르므로 에러 발생

---------------------------------------------------------------------------

ValueError                                Traceback (most recent call last)

Cell In[166], line 1
----> 1 x + z # 차원 구조가 다르므로 에러 발생

ValueError: operands could not be broadcast together with shapes (3,2,3) (3,3,2)

  
a = np.arange(6).reshape(2,3)
a.shape

(2, 3)

  
x.shape, a.shape

((3, 2, 3), (2, 3))

  
print(x,end = "\n==========\n")
print(a)

[[[ 0  1  2]
  [ 3  4  5]]

 [[ 6  7  8]
  [ 9 10 11]]

 [[12 13 14]
  [15 16 17]]]
==========
[[0 1 2]
 [3 4 5]]

  
x + a # a에 더미축을 추가하고 * 3을 수행함

array([[[ 0,  2,  4],
        [ 6,  8, 10]],

       [[ 6,  8, 10],
        [12, 14, 16]],

       [[12, 14, 16],
        [18, 20, 22]]])

dev-course, 수업 내용