파이썬 자료구조 - 스택,큐,덱
스택
스택(Stack)이란?
데이터를 저장하고 검색하는 데 사용되는 자료구조 중 하나로, LIFO(Last In First Out) 데이터 관리 방식을 따른다. 즉, 가장 나중에 들어온 데이터순으로 제거하는 방식이다.
스택 메소드
파이썬에서 일반적인 스택은 list(리스트) 자료구조로 구현이 가능하며, push(), pop() 메소드만을 지원한다. Java나 C++에서의 스택은 나머지 메소드들을 지원한다.
- push() : 데이터를 스택에 추가한다.
- pop() : 현재 담겨있는 데이터 중 가장 최근에 삽입된 데이터를 제거하여 반환한다.
- size() : 현재 스택에 담겨있는 데이터의 개수를 출력한다.
- top() : 가장 최근의 삽입된 데이터를 출력한다.
- empty() : 스택에 데이터가 없는지 여부를 출력한다.
파이썬 스택 구현 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Stack():
def __init__(self):
self.stack = list()
def push(self,num):
self.stack.append(num)
def pop(self):
if self.stack:
print(self.stack.pop())
else:
print(-1)
def size(self):
print(len(self.stack))
def top(self):
if self.stack:
print(self.stack[-1])
else:
print(-1)
def empty(self):
if self.stack:
print(0)
else:
print(1)
스택 장/단점
- 장점
- 간단한 구현 : 리스트를 활용하여 쉽게 구현 가능하다.
- 빠른 최근 데이터 접근 : LIFO 방식으로 데이터를 관리하기에, 가장 최근의 데이터에 대한 접근이 빠르다.
- 단점
- 크기 제한 : 파이썬의 리스트는 동적 배열로 구현되어 있다. 데이터가 증가하여 리스트가 꽉 차면, 리스트의 9/8배 크기 만큼 동적 할당되어 메모리에 적재된다. 따라서 메모리 소비에 주의해야한다.
- 느린 데이터 검색 : LIFO 특성에 따라 가장 최근 데이터가 아닌 데이터들에 접근하기 위해서는, 그만큼 요소를 거쳐야하므로 검색 연산이 느리다.
큐
큐(Queue)란?
스택과는 반대인 FIFO(First In First Out) 데이터 관리 방식을 따른다. 즉, 먼저 들어온 데이터순으로 제거하는 방식이다.
큐 메소드
- push() : 데이터를 큐에 추가한다.
- pop() : 삽입된 데이터 순으로 제거하여 출력한다.
- size() : 현재 큐에 담겨있는 데이터의 개수를 출력한다.
- front() : 가장 나중에 삽입된 데이터를 출력한다.
- back() : 가장 먼저 삽입된 데이터를 출력한다.
- empty() : 큐에 데이터가 없는지 여부를 출력한다.
파이썬 큐 구현 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
class Queue():
def __init__(self):
self.queue = list()
def push(self,number):
self.queue.append(number)
def pop(self):
if self.queue:
print(self.queue.pop(0))
else:
print(-1)
def size(self):
print(len(self.queue))
def empty(self):
if self.queue:
print(0)
else:
print(1)
def front(self):
if self.queue:
print(self.queue[0])
else:
print(-1)
def back(self):
if self.queue:
print(self.queue[-1])
else:
print(-1)
리스트를 활용하여 큐를 구현하였다. 비록 기능은 같을지 몰라도 시간면에서는 완전히 다르다. 0부터 9까지의 리스트가 있다고 가정하자. 앞서 말한것처럼 파이썬의 리스트는 동적 배열로 구현되어 있다. 만약 pop(0) 을 수행하면, 아래와 같이 0이 삭제될 것이다.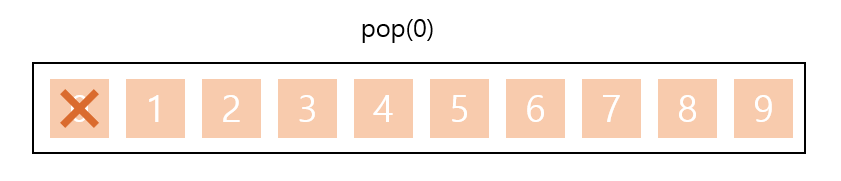 
리스트 pop(0) 수행
그럼 해당 리스트는 삭제된 원소의 자리를 채우기위해 다음 원소(데이터)부터 차례대로 이동된다. 따라서 총 9번의 이동 연산이 수행된다.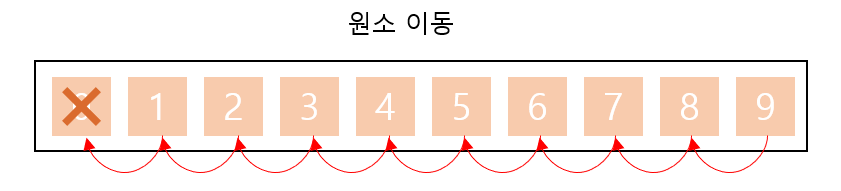 
리스트 원소 이동
위와 같이 기본적인 큐의 pop()연산은 \(O(1)\) 인데 반해, 파이썬 리스트의 pop(0)연산은 데이터 개수-1 즉, \(O(N)\)이 되는 셈이다. 따라서 파이썬에서는 queue 모듈이나 이후 설명할 덱(deque) 모듈을 사용한다.
큐의 장/단점
- 장점
- 데이터 순서 보장 : FIFO 방식으로 데이터를 관리하기에, 순차적인 데이터 처리에 유용하다.
- 선택적 크기 제한 : 내장 모듈인 queue를 통해 큐의 최대 용량을 설정할 수 있다.
- 단점
- 메모리 사용량 : 스택과 마찬가지로 데이터를 저장하는데 메모리를 사용하므로, 데이터가 증가할수록 메모리 사용량이 증가될 수 있다.
- 느린 데이터 검색 : FIFO 특성에 따라 가장 삽입된 데이터가 아닌 데이터들에 접근하기 위해서는, 그만큼 요소를 거쳐야하므로 검색 연산이 느리다.
덱
덱(Deque)이란?
더블 엔디드 큐(Double-Ended Queue)의 줄임말로, 양쪽에서 삽입과 삭제를 모두 처리할 수 있어 스택과 큐의 특징을 모두 가진 자료구조이다. 이중 연결 리스트(Doubly Linked List)로 구현되어 있어 양쪽에서의 연산이 \(O(1)\)의 시간 복잡도로 빠르게 수행된다.
덱 메소드
파이썬 내장 모듈인 collections의 deque 클래스 주요 메소드이다.
- appendleft() : 덱의 왼쪽(맨 앞)에 데이터를 추가한다.
- append() : 덱의 오른쪽(맨 끝)에 데이터를 추가한다.
- popleft() : 덱의 왼쪽 끝에 있는 데이터를 제거하고 반환한다.
- pop() : 덱의 오른쪽 끝에 있는 데이터를 제거하고 반환한다.
- extend(iterable) : 덱의 오른쪽 끝에 iterable 요소들을 모두 추가한다.
- extendleft(iterable) : 덱의 왼쪽 끝에 iterable 요소들을 모두 추가한다.
- rotate(n) : n이 양수면 오른쪽으로, 음수면 왼쪽으로 덱을 회전한다. 주로 원형 큐 구현에 사용한다.
파이썬 덱 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
from collections import deque
dq = deque([i for i in range(10)])
## appendleft()
dq.appendleft(50)
print(dq)
"""
결과
>>> deque([50, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
"""
## append()
dq.append(100)
print(dq)
"""
결과
>>> deque([50, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 100])
"""
## popleft()
print(dq.popleft())
"""
결과
>>> 50
"""
## pop()
print(dq.pop())
"""
결과
>>> 100
"""
## extend()
dq.extend([200,300])
print(dq)
"""
결과
>>> deque([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 200, 300])
"""
## extendleft()
dq.extendleft([-10,-20])
print(dq)
"""
결과
>>> deque([-20, -10, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 200, 300])
"""
## rotate()
dq.rotate(2)
print(dq)
"""
결과
>>> deque([200, 300, -20, -10, 0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
"""
dq.rotate(-4)
print(dq)
"""
결과
>>> deque([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 200, 300, -20, -10])
"""
활용 예시
스택,큐,덱 모두 데이터를 저장한다는점에서는 동일하지만, 삽입·삭제 연산을 통한 관리 방식에서는 차이가 있다. 그럼 어떠한 경우 해당 자료구조를 활용해야 하는지 알아보았다.