파이썬 자료구조 - 트리

트리

트리(Tree)란?

계층형 트리 구조를 시뮬레이션 하는 추상 자료형으로, 루트(Root)값과 부모-자식 관계의 서브트리(Subtree)로 구성되며, 서로 연결된 노드의 집합이다

트리 용어

트리

• 노드(Node) : 트리를 구성하는 기본 원소
  • 루트 노드(Root Node) : 트리의 시작점인 노드. 최상위 레벨
  • 부모 노드(Parent Node) : 하위 계층으로 연결된 노드가 있는 상위 노드
  • 자식 노드(Child Node) : 상위 계층으로 연결된 노드가 있는 하위 노드
  • 리프 노드(Leaf Node) : 자식노드가 없는 노드. 최하위 레벨
  • 형제 노드(Siblings Node) : 같은 부모 노드를 갖는 노드들
• 간선(Edge) : 노드 간의 연결선
• 차수·계수(Order) : 각 노드의 자식 노드 개수. 트리의 차수 = 가장 많은 자식 노드를 가진 개수
• 크기(Size) : 루트 노드를 포함한 노드의 개수
• 깊이(Depth) : 루트 노드에서 해당 노드까지의 길이. 즉 루트 노드에서 해당 노드까지 몇개의 간선을 거치는지를 의미
• 높이(Height) : 최하위 리프 노드를 기준으로 해당 노드의 길이. 최대 깊이는 곧 최대 높이와 같음
• 레벨(Level) : 같은 깊이(혹은 높이)를 가지고 있는 노드를 묶어서 레벨로 표현. 간혹 루트 노드를 1 혹은 0으로 시작
• 서브트리(Sub-Tree) : 한 개 이상의 노드로 이루어진 부분 트리 집합

트리 특성

• 트리는 그래프의 일종으로, 비순환 구조를 가진다.
  • 그림과 같이, 트리는 그래프와 달리, 어떤 노드에서 시작하여 자기 자신으로 돌아오는 경로가 없다. 트리·그래프 차이
• 루트 노드는 반드시 하나만 존재한다.
• 어떤 노드에 대하여, 부모 노드는 반드시 하나만 존재한다.
• 트리의 간선 개수는 총 노드 개수 N에 대하여 N-1개이다.

이진 트리

모든 노드의 자식 노드 개수(차수)가 2 이하인 경우, 이를 이진 트리로 칭한다.

이진 트리 유형

이진 트리 유형

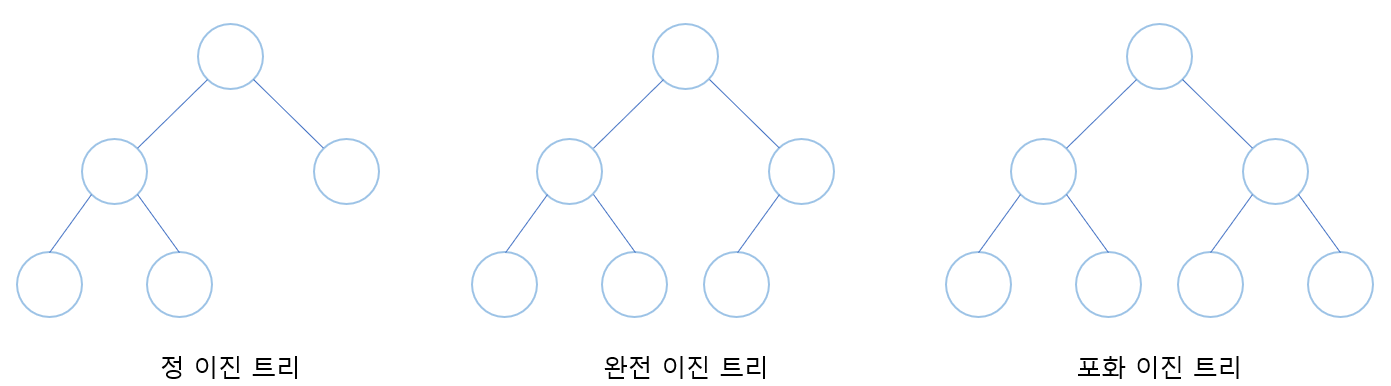
• 정 이진 트리(Full Binary Tree) : 모든 노드가 0개 또는 2개 자식 노드를 지님
• 완전 이진 트리(Complete Binary Tree) : 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가장 왼쪽부터 채워져 있음
• 포화 이진 트리(Perfect Binary Tree) : 모든 노드가 2개의 자식 노드를 갖고 있으며, 모든 리프 노드가 동일한 깊이 혹은 레벨을 갖음

이진 트리 순회 유형

이진 트리 순회

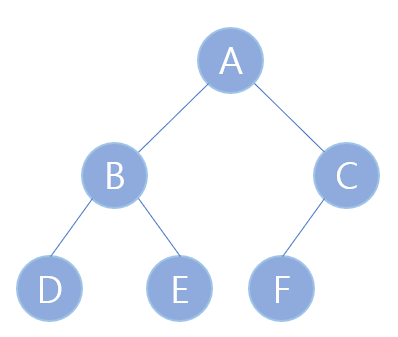
• 전위 순회(preorder traversal) : \(루트 \rightarrow 왼쪽 자식 노드 \rightarrow 오른쪽 자식 노드\)
  • 위 트리의 전위 순회 결과는 A - B - D - E - C - F
• 중위 순회(inorder traversal) : \(왼쪽 자식 노드 \rightarrow 루트 \rightarrow 오른쪽 자식 노드\)
  • 위 트리의 중위 순회 결과는 D - B - E - A - F - C
• 후위 순회(postorder traversal) : \(왼쪽 자식 노드 \rightarrow 오른쪽 자식 노드 \rightarrow 루트\)
  • 위 트리의 후위 순회 결과는 D - E - B - F - C - A